Encryption
How to use the slides - Full screen (new tab)
Encryption
Goals for this lesson
- Learn about the differences between symmetric and asymmetric encryption.
Symmetric Cryptography
Symmetric encryption assumes all parties begin with some shared secret information, a potentially very difficult requirement.
The shared secret can then be used to protect further communications from others who do not know this secret.
In essence, it gives a way of extending a shared secret over time.
Symmetric Encryption
Examples: ChaCha20, Twofish, Serpent, Blowfish, XOR, DES, AES
Symmetric Encryption API
Symmetric encryption libraries should generally all expose some basic functions:
fn generate_key(r) -> k;
Generate ak(secret key) from some inputr.fn encrypt(k, msg) -> ciphertext;
Takeskand a message; returns the ciphertext.fn decrypt(k, ciphertext) -> msg;
Takeskand a ciphertext; returns the original message.
It always holds that decrypt(k, encrypt(k, msg)) == msg.
Notes:
The input r is typically a source of randomness, for example the movement pattern of a mouse.
Symmetric Encryption Guarantees
Provides:
- Confidentiality
- Authenticity*
Does not provide:
- Integrity*
- Non-Repudiation
Notes:
- Authenticity: The message could only be sent by someone who knows the shared secret key. In most cases, this is functionally authentication to the receiving party.
- Integrity: There is no proper integrity check, however the changed section of the message will be gibberish if it has been changed. Detection of gibberish could function as a form of integrity-checking.
Non-repudiation for Symmetric Encryption
There is cryptographic proof that the secret was known to the producer of the encrypted message.
However, knowledge of the secret is not restricted to one party: Both (or all) parties in a symmetrically encrypted communication know the secret. Additionally, in order to prove this to anyone, they must also gain knowledge of the secret.
Notes:
The degree of non-repudiation given by pure symmetric crytography is not very useful.
Symmetric Encryption
Example: XOR Cipher
The encryption and decryption functions are identical: applying a bitwise XOR operation with a key.
Plain: 1010 -->Cipher: 0110
Key: 1100 | 1100
---- | ----
0110--^ 1010
Notes:
A plaintext can be converted to ciphertext, and vice versa, by applying a bitwise XOR operation with a key known to both parties.
Symmetric Encryption
⚠ Warning ⚠
We typically expect symmetric encryption to preserve little about the original plaintext. We caution however that constructing these protocols remains delicate, even given secure primitives, with two classical examples being unsalted passwords and the ECB penguin.
ECB penguin

Original image
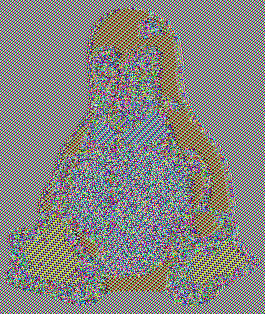
Encrypted image
(by blocks)

Encrypted image
(all at once)
Notes:
The ECB penguin shows what can go wrong when you encrypt a small piece of data, and do this many times with the same key, instead of encrypting data all at once.
Image sources: https://github.com/robertdavidgraham/ecb-penguin/blob/master/Tux.png and https://github.com/robertdavidgraham/ecb-penguin/blob/master/Tux.ecb.png and https://upload.wikimedia.org/wikipedia/commons/5/58/Tux_secure.png
Asymmetric Encryption
- Assumes the sender does not know the recipient's secret "key" 🎉😎
- Sender only knows a special identifier of this secret
- Messages encrypted with the special identifier can only be decrypted with knowledge of the secret.
- Knowledge of this identifier does not imply knowledge of the secret, and thus cannot be used to decrypt messages encrypted with it.
- For this reason, the identifier may be shared publicly and is known as the public key.
Asymmetric Encryption

Why "Asymmetric"?
Using only the public key, information can be transformed ("encrypted") such that only those with knowledge of the secret are able to inverse and regain the original information.
i.e. Public key is used to encrypt but a different, secret, key must be used to decrypt.
Asymmetric Encryption API
Asymmetric encryption libraries should generally all expose some basic functions:
fn generate_key(r) -> sk;
Generate ask(secret key) from some inputr.fn public_key(sk) -> pk;
Generate apk(public key) from the private keysk.fn encrypt(pk, msg) -> ciphertext;
Takes the public key and a message; returns the ciphertext.fn decrypt(sk, ciphertext) -> msg;
For the inputsskand a ciphertext; returns the original message.
It always holds that decrypt(sk, encrypt(public_key(sk), msg)) == msg.
Notes:
The input r is typically a source of randomness, for example the movement pattern of a mouse.
Asymmetric Encryption Guarantees
Provides:
- Confidentiality
Does not provide:
- Integrity*
- Authenticity
- Non-Repudiation
Notes:
- Authenticity: The message could only be sent by someone who knows the shared secret key. In most cases, this is functionally authentication to the receiving party.
- Integrity: There is no proper integrity check, however the changed section of the message will be gibberish if it has been changed. Detection of gibberish could function as a form of integrity-checking.
Diffie-Hellman Key Exchange

Mixing Paint Visualization
Notes:
Mixing paint example. Image Source: https://upload.wikimedia.org/wikipedia/commons/4/46/Diffie-Hellman_Key_Exchange.svg
Authenticated Encryption
Authenticated encryption adds a Message Authentication Code to additionally provide an authenticity and integrity guarantee to encrypted data.
A reader can check the MAC to ensure the message was constructed by someone knowing the secret.
Notes:
Specifically, this authenticity says that anyone who does not know the sender's secret could not construct the message.
Generally, this adds ~16-32 bytes of overhead per encrypted message.
AEAD (Authenticated Encryption Additional Data)
AEAD is authenticated with some extra data which is unencrypted, but does have integrity and authenticity guarantees.
Notes:
Authenticated encryption and AEAD can work with both symmetric and asymmetric cryptography.
AEAD Example
Imagine a table with encrypted medical records stored in a table, where the data is stored using AEAD. What are the advantages of such a scheme?
UserID -> Data (encrypted), UserID (additional data)
Notes: By using this scheme, the data is always associated with the userID. An attacker could not put that entry into another user's entry.
Hybrid Encryption
Hybrid encryption combines the best of all worlds in encryption. Asymmetric encryption establishes a shared secret between the sender and a specific public key, and then uses symmetric encryption to encrypt the actual message. It can also be authenticated.
Notes:
In practice, asymmetric encryption is almost always hybrid encryption.
Cryptographic Properties
| Property | Symmetric | Asymmetric | Authenticated | Hybrid + Authenticated |
|---|---|---|---|---|
| Confidentiality | Yes | Yes | Yes | Yes |
| Authenticity | Yes* | No | Yes* | Yes |
| Integrity | No* | No* | Yes | Yes |
| Non-repudiation | No | No* | No | No* |
Notes:
- Symmetric-Authentication and Authenticated-Authenticity: The message could only be sent by someone who knows the shared secret key. In most cases, this is functionally authentication to the receiving party.
- Symmetric-Integrity and Asymmetric-Integrity: There is no proper integrity check, however the message will be gibberish if it has been changed. Detection of gibberish could function as a form of integrity-checking.
- Non-Repudation: Even though none of these primitives provide non-repudiation on their own, it's very possible to add non-repudation to asymmetric and hybrid schemes via signatures.
- Note that encryption also, most importantly, makes the data available to everyone who should have access.