Data Availability and Sharding

Data Availability and Sharding

Outline

Data Availability Problem

How do we ensure a piece of data is retrievable without storing it on every single node forever?

Incorrectness can be proven (fraud proofs), but unavailability can't.

---v

Data Availability Problem: Parachains

Imagine a parachain collator produces a block, but only sends it to relay chain validators to verify.

What could such a collator do?

We want other collators to be able to reconstruct the block from the relay chain.

---v

Data Availability Problem: Relay Chain

If that block's PoV is only stored by a few validators, what if they go offline or rogue?

Notes:

This is really bad. It means we could finalize an invalid parachain block.

Problem

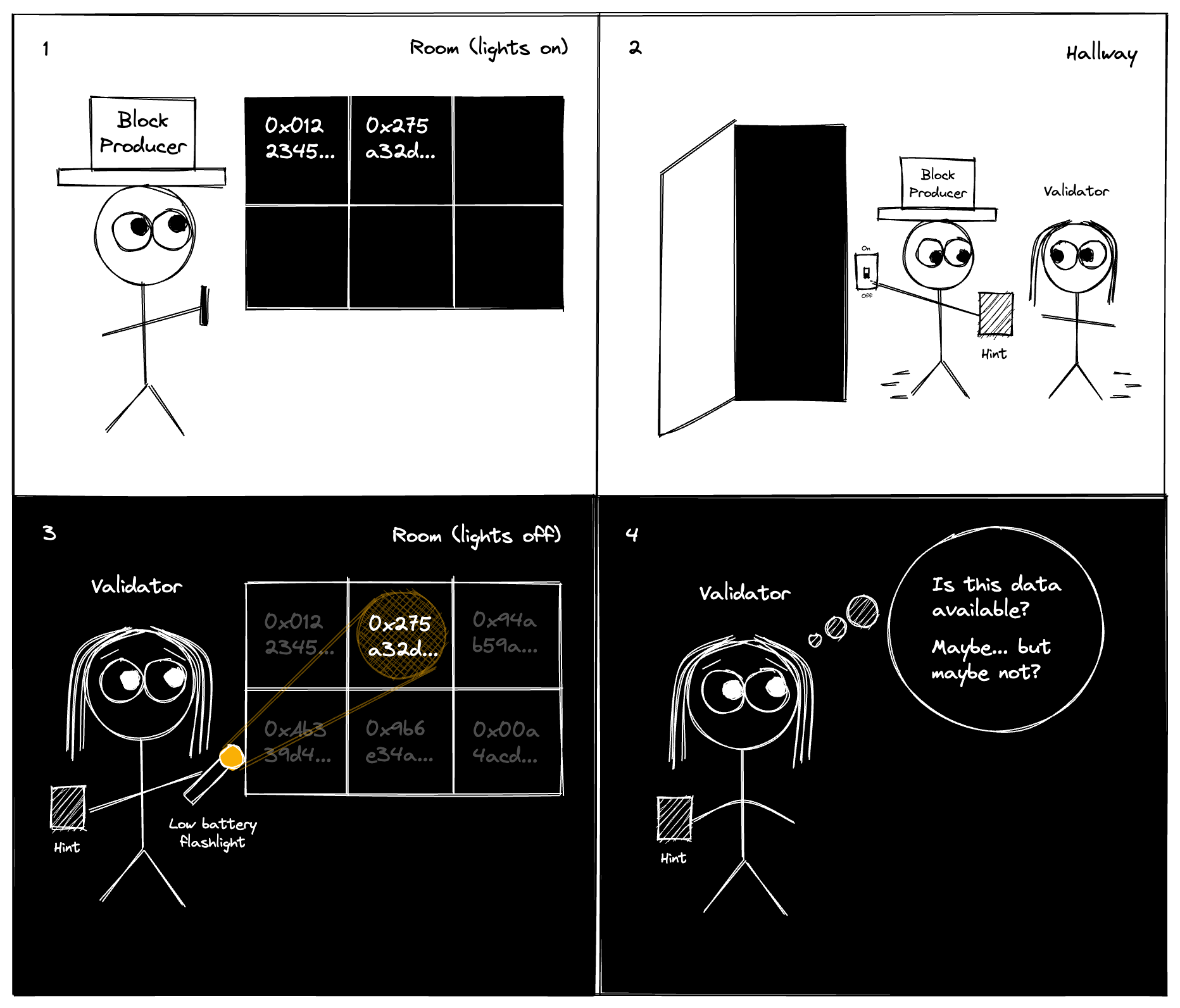
Notes:

I really like this comic from the paradigm article about Data Availability Sampling. But it works for our case as well with data sharding.

Erasure coding

The goal:

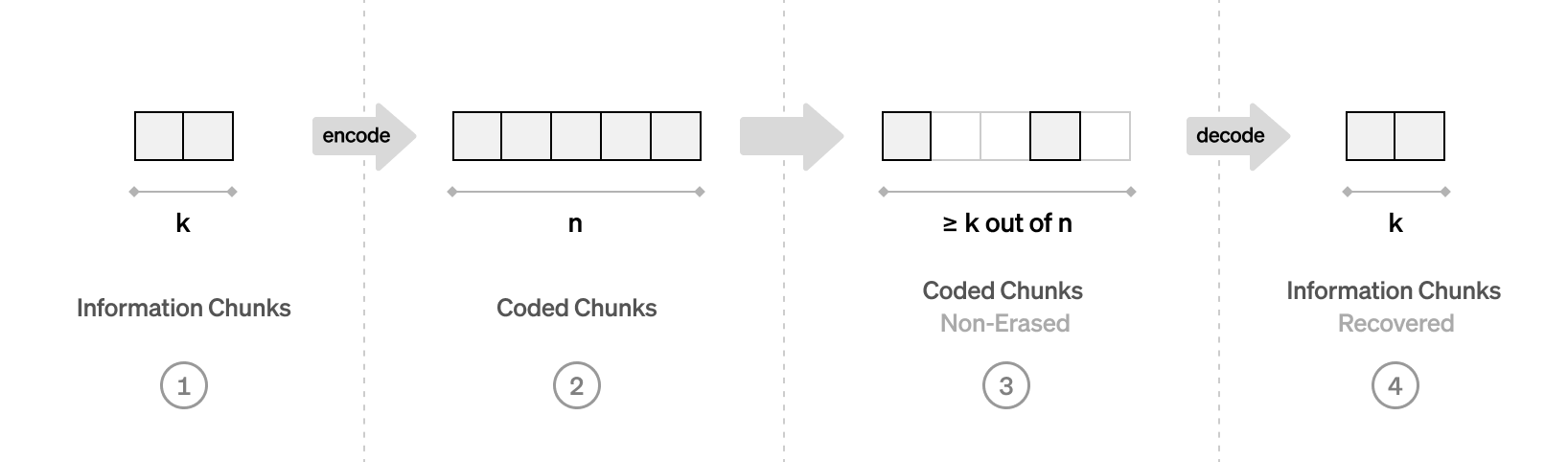
---v

In code

#![allow(unused)]
fn main() {
type Data = Vec<u8>;

pub struct Chunk {
	pub index: usize,
	pub bytes: Vec<u8>,
}

pub fn encode(_input: &Data) -> Vec<Chunk> {
	todo!()
}

pub fn reconstruct(_chunks: impl Iterator<Item = Chunk>) -> Result<Data, Error> {
	todo!()
}
}

Polynomials

---v

Polynomials: Line

---v

Even More Polynomials

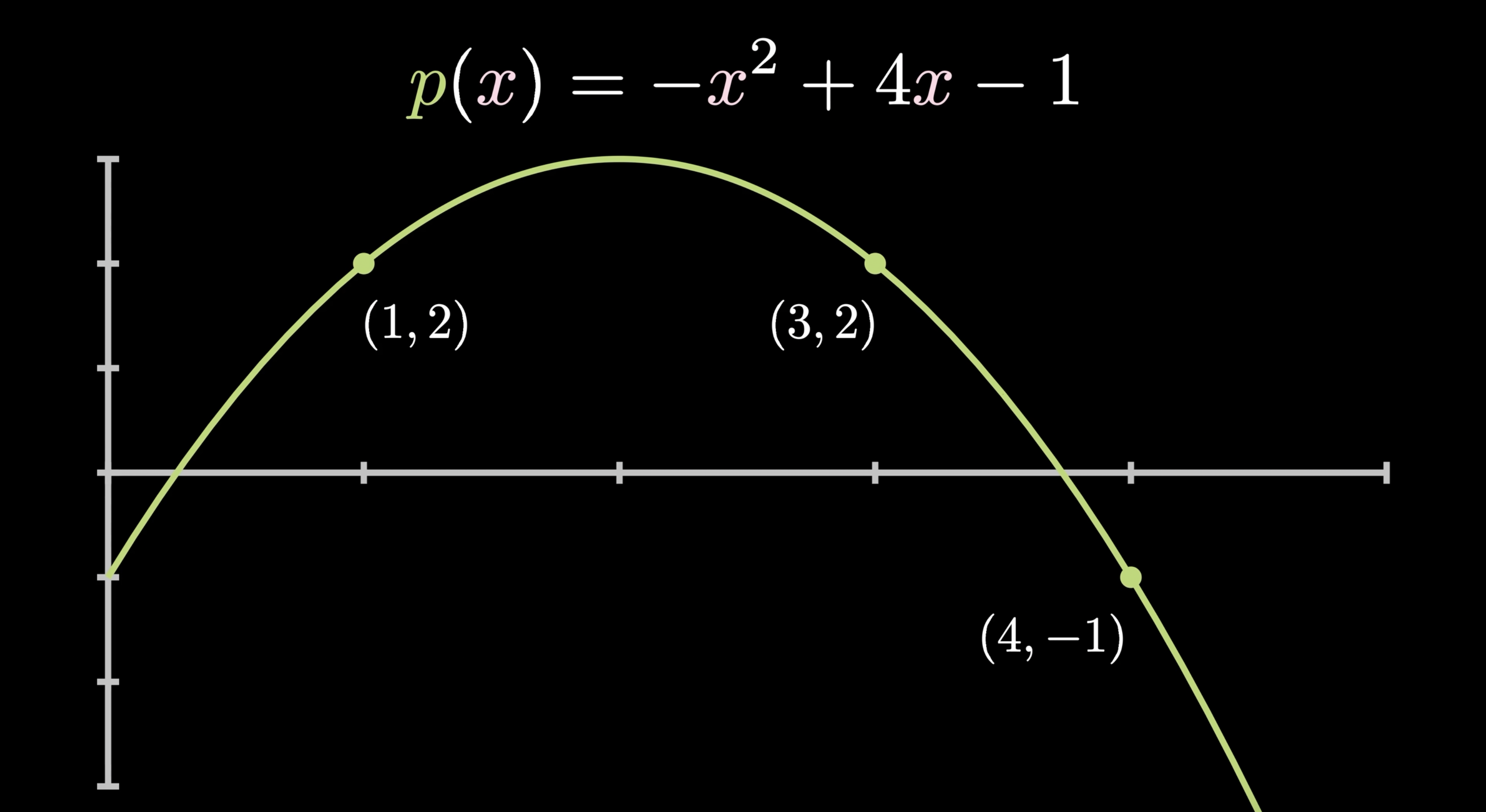
---v

Polynomial we need

We want to have a polynomial, such that:

$$ p(x_i) = y_i$$

Notes:

Question: what is x_i and y_i wrt to our data?

Lagrange interpolating polynomial

$$ \ell_j(x) = \frac{(x-x_0)}{(x_j-x_0)} \cdots \frac{(x-x_{j-1})}{(x_j-x_{j - 1})} \frac{(x-x_{j+1})}{(x_j-x_{j+1})} \cdots \frac{(x-x_k)}{(x_j-x_k)} $$

$$ L(x) = \sum_{j=0}^{k} y_j \ell_j(x) $$

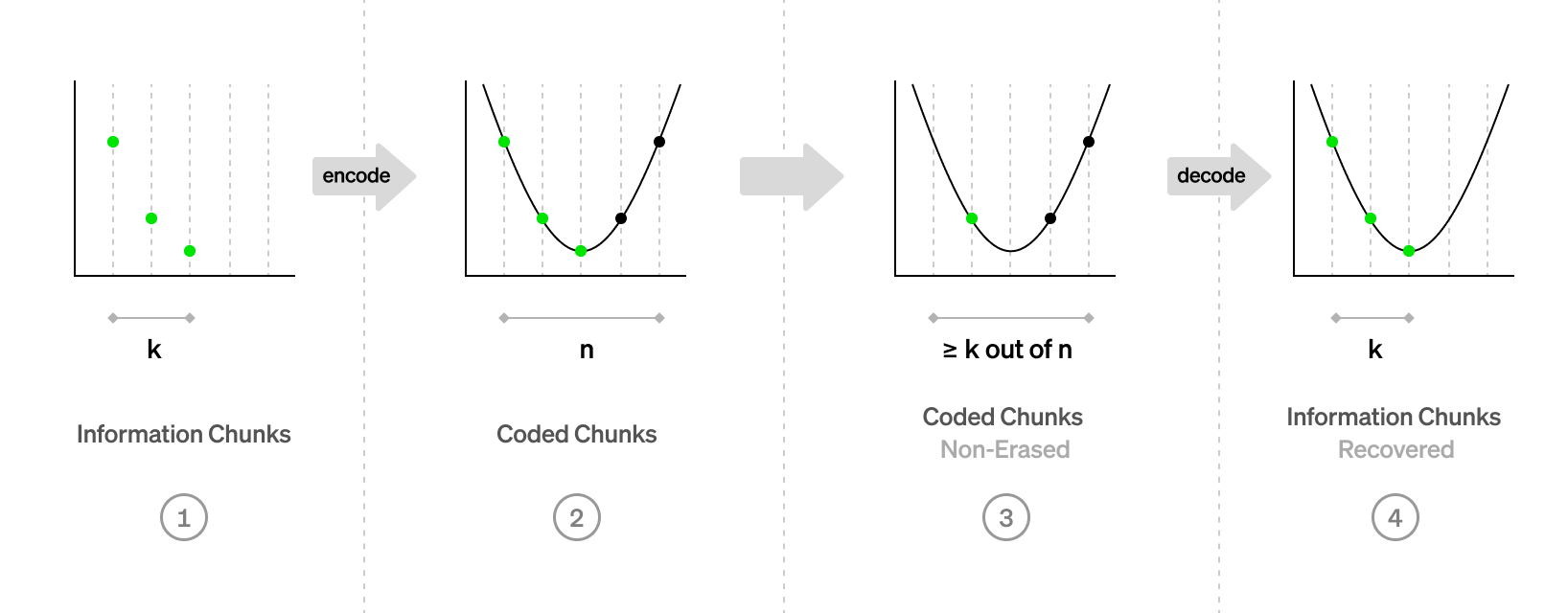
Reed-Solomon codes

Congrats! You've just learned Reed-Solomon encoding (almost).

Actual Reed-Solomon codes are defined over finite-fields.

It can detect and correct combinations of errors and erasures.

Notes:

The simplest example of a finite field is arithmetic mod prime number. Computers are quite bad at division by prime numbers. Reed-Solomon codes are used in CDs, DVDs, QR codes and RAID 6.

---v

Reed-Solomon with Lagrange interpolation

1. Divide the data into elements of size $P$ bits.
2. Interpret the bytes as (big) numbers $\mod P$.
3. Index of each element is $x_i$ and the element itself is $y_i$.
4. Construct the interpolating polynomial $p(x)$ and evaluate it at additional $n - k$ points.
5. The encoding is $(y_0, ..., y_{k-1}, p(k), ... p(n - 1))$ along with indices.

Notes:

How do we do reconstruction?

Polkadot's Data Availability Protocol

Notes:

The total amount of data stored by all validators is PoV * 3. With 5MB PoV and 1k validators, each validator only stores 15KB per PoV. With this protocol, we've killed two birds with one stone!

CandidateIncluded

Availability Bitfields

Notes:

Each validator actually signs a statement per relay chain block, not per PoV to reduce the number of signatures. These statements are gossiped off-chain and included in a block in a ParachainsInherent.

Challenge 1

How does a validator know if a chunk corresponds to the committed data?

---v

Not that Merkle!

Challenge 2

How do we know if what can be reconstructed from chunks is the same data that was encoded with Reed-Solomon?

Data Availability Sampling

Ethereum (Danksharding) and Celestia adopt an approach of Data Availability Sampling, where each light client makes its own judgement of availability by sampling and distributing a few random chunks.

This can eliminate honest majority assumption!

This approach guarantees there's at least one honest full nodes that has the data with high probability.

https://arxiv.org/abs/1809.09044

Safety of Polkadot's protocol

If we have at most $f$ out of $3f + 1$ malicious + offline validators, then if the data is marked as available, it can be recovered.

What if that assumption is broken?

If $2f + 1$ are malicious, every PoS is doomed anyway.

Notes:

We'll see in the next lesson, how approval-voting can prevent unavailable blocks from being finalized even with $>f$ malicious nodes.

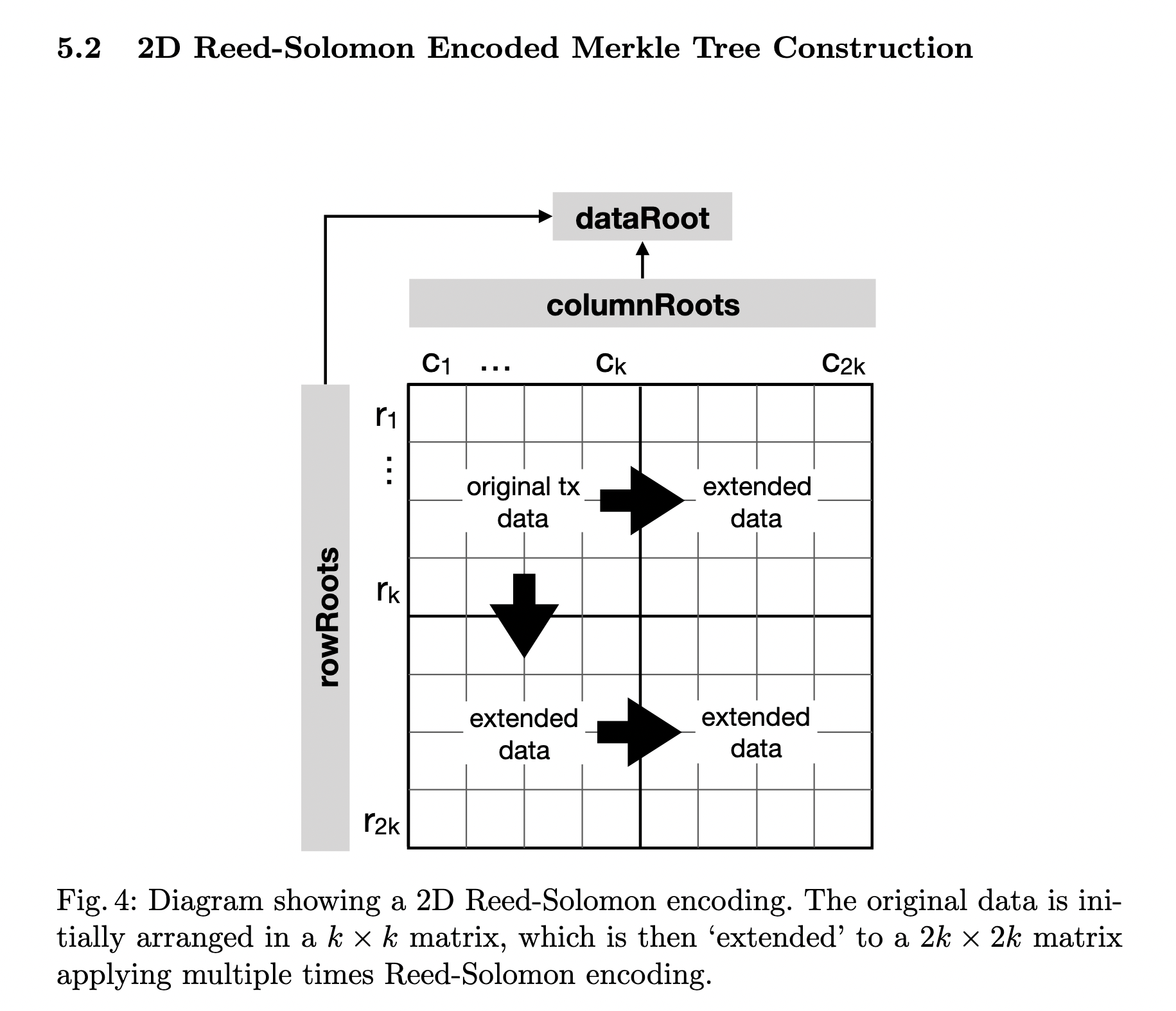
2D Reed-Solomon Encoding

Notes:

The approach of 2D Reed-Solomon Encoding can reduce the size of a Fraud Proof used by Celestia. But it adds an overhead computationally and on the amount of data stored.

Comparison with other approaches

• Both Danksharding and Celestia use 2D encoding and DAS
• Celestia doesn't implement data sharding
• Data availability is only part of ensuring validity
• Polkadot's DA is able to process dozens of MB per second

Notes:

Danksharding is aiming at 1.3 MB/s and Celestia < 1 MB/s.

Ideas to Explore

Questions

Bonus

https://github.com/paritytech/reed-solomon-novelpoly

References

1. https://www.youtube.com/watch?v=1pQJkt7-R4Q
2. https://notes.ethereum.org/@vbuterin/proto_danksharding_faq
3. https://www.paradigm.xyz/2022/08/das