Introduction to Cryptography

Introduction to Cryptography

Some Useful Equations

Notes:

Just kidding!

Goals for this lesson

Notes:

In this first lesson,

Cryptography Landscape

Notes:

What is covered in this course is all connected subjects. We will not cover any details for hybrid or interactive protocols in the course.

Operating Context

The internet is a public space.

We communicate over public channels. Adversaries may want to:

Notes:

Use e-mail as an example of an flawed system.

Some examples include:

• An attacker may impersonate your boss, trying to get you to send them money
• An attacker may change a message sent over a network, e.g. an instruction to transfer 100 EUR to 10000 EUR

Probably best for the teacher to ask students to participate with examples of application messages, not just person-to-person messages.

Operating Context

Resources are constrained.

• Network, storage, computation, etc.: We don't want to send, store, or operate on the same data, but we want guarantees about it, e.g. that we agree on a message's contents.
• Privacy: We must assume that all channels can be monitored, and thus closed channels are heavily constrained (i.e. assumed to not exist).

Open vs. Closed Channels

Cryptography based on public systems is more sound.

Kerckhoff's Principle: Security should not rely on secret methods,
but rather on secret information.

Notes:

There is no such thing as a "closed channel" :)

• Methods can be reverse engineered. After that, the communication channel is completely insecure. For example, CSS protection for DVDs.
• We always work with public, open protocols.

Cryptographic Guarantees*

Notes:

Cryptography is one of the (most important) tools we have to build tools that are guaranteed to work correctly. This is regardless of who (human, machine, or otherwise) is using them and their intentions (good or bad).

Why an asterisk? There generally are no perfect & absolute guarantees here, but for most practical purposes the bounds on where these fail are good enough to serve our needs as engineers and users. Do note the assumptions and monitor their validity over time (like quantum tech).

Important Non-Guarantee

Cryptography alone cannot make strong guarantees that data is available to people when they want to access it.

Notes:

There are many schemes to get around this, and this topic will come up later in the course. We will touch on erasure coding, which makes data availability more efficient.

Data Confidentiality

A party may gain access to information
if and only if they know some secret (a key).

Confidentiality ensures that a third party cannot read my confidential data.

Notes:

The ability to decrypt some data and reveal its underlying information directly implies knowledge of some secret, potentially unknown to the originator of the information. Supplying the original information (aka plain text message) can be used in a "challenge game" mechanism as one means of proving knowledge of the secret without compromising it.

Mention use of the term "plaintext".

Allegory: A private document stored on server where sysadmin has access can be subpoenaed, violating assumed Attorney-Client Privilege on the document.

---v

Confidentiality in Communication Channels

Suppose Alice and Bob are sending confidential messages back and forth. There are some subtypes of confidentiality here:

• Forward Secrecy: Even if an adversary temporarily learns Alice's secret, it cannot read future messages after some point.
• Backwards Secrecy: Even if an adversary temporarily learns Alice's secret, it cannot read past messages beyond some previous point.

Data Authenticity

Users can have the credible expectation that the stated origin of a message is authentic.

Authenticity ensures that a third party cannot pretend I created some data.

Notes:

• Digital signatures should be difficult (practically speaking: impossible) to forge.
• Digital signatures should verify that the signer knows some secret, without revealing the secret itself.

Data Integrity

If data is tampered with, it is detectable. In other words, it possible to check if the current state of some data is the consistent with when it was created.

Integrity ensures that if data I create is corrupted, it can be detected.

---v

Physical Signatures

Physical signatures provide weak authenticity guarantees
(i.e. they are quite easy to forge), and no integrity guarantees.

---v

An Ideal Signature

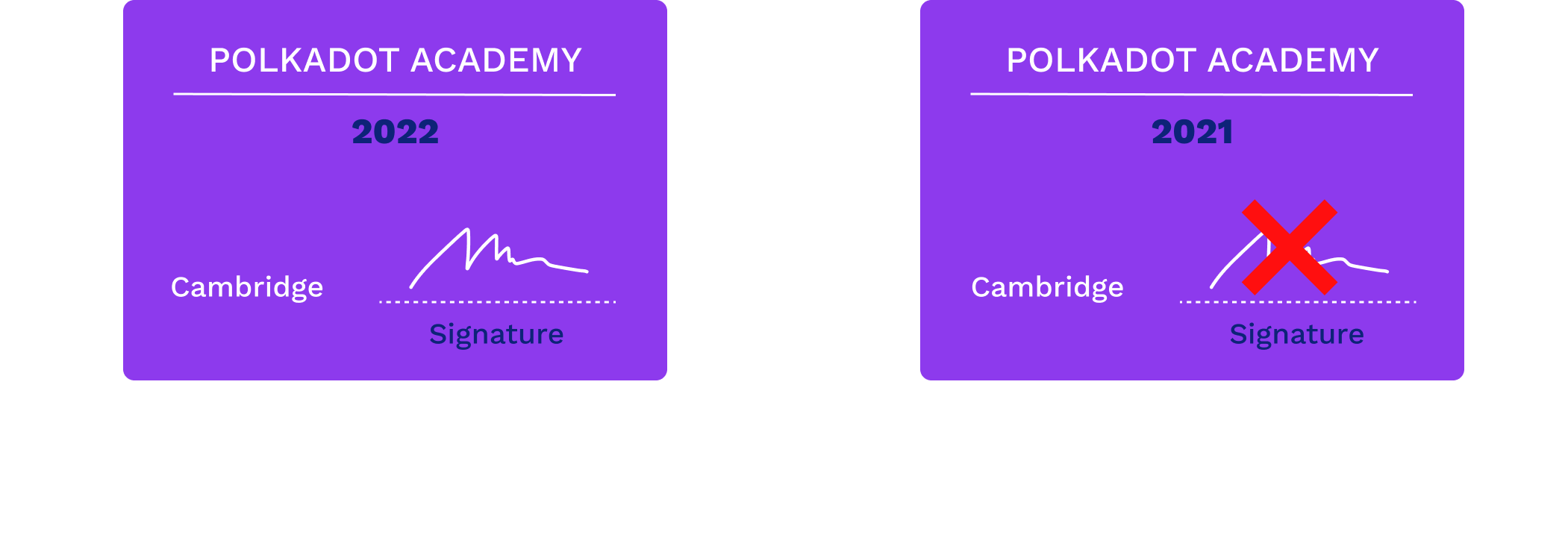
Notes:

For example, if you change the year on your university diploma, the dean's signature is still valid. Digital signatures provide a guarantee that the signed information has not been tampered with.

Non-repudiation

The sender of a message cannot deny that they sent it.

Non-repudiation ensures if Bob sends me some data, I can prove to a third party that they sent it.

One-Way Functions

One-way functions form the basis of both
(cryptographic) hashing and asymmetric cryptography. A function $f$ is one way if:

• it is reasonably fast to compute
• it is very, very slow to undo

Notes:

There are a lot of assumptions about why these functions are hard to invert, but we cannot rigorously prove it. We often express inversion problems in terms of mathematical games or oracles.

Hash Functions

Motivation: We often want a succinct, yet unique representation of some (potentially large) data.

A fingerprint, which is much smaller than a person, yet uniquely identifies an individual.

Notes:

The following slides serve as an intro. Many terms may be glossed over, and covered in detail later. There are lessons later in this module dedicated to hashes and hash-based data structures.

---v

Hash Function Applications

Hashes can be useful for many applications:

Symmetric Cryptography

Symmetric encryption assumes all parties begin with some shared secret information, a potentially very difficult requirement.
The shared secret can then be used to protect further communications from others who do not know this secret.

In essence, it gives a way of extending a shared secret over time.

Notes:

Remember that these communications are over an open channel, as we assumed that all channels can be monitored.

Symmetric Encryption

For example, the Enigma cipher in WW2. A channel was initiated by sharing a secret ("key") between two participants. Using the cipher, those participants could then exchange information securely.

However, since the key contained only limited entropy ("information"), enough usage of it eventually compromised the secret and allowed the allies to decode messages. Even altering it once per day was not enough.

Notes:

When communicating over a channel that is protected with only a certain amount of entropy, it is still possible to extend messages basically indefinitely by introducing new entropy that is used to protect the channel sufficiently often.

Asymmetric Cryptography

• In asymmetric cryptography, we devise a means to transform one value (the "secret") into some corresponding counterpart (the "public" key), preserving certain properties.

• We believe that this is a one-way function (that there is no easy/fast inverse of this function).

• Aside from preserving certain properties, we believe this counterpart (the "public key") reveals no information about the secret.

Asymmetric Encryption

Using only the public key, information can be transformed ("encrypted") such that only those with knowledge of the secret are able to inverse and regain the original information.

Digital Signatures

• Using the secret key, information can be transformed ("signed") such that anyone with knowledge of the information and the counterpart public key is able to affirm the operation.

• Digital signatures provide message authenticity and integrity guarantees.

• There are two lessons are dedicated to digital signatures,
  this is strictly an intro.

Digital Signatures

Signing function: a function which operates on some
message data and some secret to yield a signature.

A signature proves that the signer had knowledge of the secret,
without revealing the secret itself.

The signature cannot be used to create other signatures, and is unique to the message.

Notes:

A signing function is a pure function which operates on some message data (which may or may not be small, depending on the function) and some secret (a small piece of information known only to the operator). The result of this function is a small piece of data called a signature.

Pure means that it has no side effects.

It has a special property: it proves (beyond reasonable doubt) that the signer (i.e. operator of the signing function) had knowledge of the secret and utilized this knowledge with the specific message data, yet it does not reveal the secret itself, nor can knowledge of the signature be used to create other signatures (e.g. for alternative message data).

Non-repudiation for Crypgraphic Signatures

There is cryptographic proof that the secret was known to the producer of the signature.

The signer cannot claim that the signature was forged, unless they can defend a claim that the secret was compromised prior to signing.

Practical Considerations

Symmetric cryptography is much faster, but requires more setup (key establishment) and trust (someone else knows the secret).

Asymmetric cryptography is slow, but typically preserves specific algebraic relationships, which then permit more diverse if fragile protocols.

Hybrid Cryptography

Hybrid cryptography composes new mechanisms from different cryptographic primitives.

For example:

• Symmetric encryption can provide speed, and often confidentiality,
• Hash functions can reduce the size of data while preserving identity,
• Asymmetric cryptography can dictate relations among the participants.

Certifications

Certifications are used to make attestations about public key relationships.

Typically in the form of a signature on:

• One or more cryptographically strong identifiers (e.g. public keys, hashes).
• Information about its ownership, its use and any other properties that the signer is capable of attesting/authorizing/witnessing.
• (Meta-)information about this information itself, such as how long it is valid for and external considerations which would invalidate it.

Notes:

• Real application is the hierarchy of SSL certs.
  • Root keys -> State level entities -> Smaller entities.
• Web of Trust & GPG cross-signing
• In the case of signature-based certificates, as long as you have the signature, data, and originating public key, you can trust a certificate no matter where it came from. It could be posted on a public message board, sent to you privately, or etched into stone.

Entropy, Randomness, and Key Size

• Entropy: Amount of non-redundant information contained within some data.
• Randomness: Unpredictability of some information. Less random implies lower entropy.
• Key size: Upper limit of possible entropy contained in a key. Keys with less random (more predictable) data have less entropy than this upper bound.
• One-time pad: A key of effectively infinite size. If it is perfectly random (i.e. has maximal entropy), then the cipher is theoretically unbreakable.

Notes:

Mention the upcoming "many time pad" activity, that exploits using a one time pad multiple times.

Randomness Generation

#![allow(unused)]
fn main() {
fn roll_die() -> u32 {
  // Guaranteed random: it was achieved through a real-life die-roll.
  4u32
}
}

• Pseudo-random sequences
• Physical data collection (e.g. cursor movement, LSB of microphone)
• Specialised hardware (e.g. low-level noise on silicon gates, quantum-amplifiers)

Notes:

LSB := Least Significant Bit

Summary

Cryptography is much more than encryption.

Questions

What insights did you gain?

Notes:

Class discussion. Last slide.