Cryptography In Context

How to use the slides - Full screen (new tab) Slides Content --- title: Cryptography In Context description: Real-world considerations around cryptography duration: 1 hour ---

Cryptography in Context

Outline

Keeping Secrets Secret
Security and Usability

Secrets

What is a secret in cryptography?

Data that you know, that nobody else knows.

How Secrets Stay Secret

In order for a cryptographic secret to stay secret, the only thing about it that can be revealed is the output of known, secured cryptographic operations.

A (sufficiently random) secret can be hashed, and the hash revealed.
A private key can be used to generate a public key, and the public key revealed.
A private key can be used to generate a signature, and the signature revealed.

How Secrets Get Leaked

Inadvertently leaking information about the secret during normal operation.
Compromised digital or physical security leading to private key loss.

Notes:

Let's go over each of these in order.

Bad Randomness

Some algorithms require randomness. If the randomness is compromised, the private key or encrypted message can possibly be exposed.

Notes:

one source

Side Channel Attacks

A side channel attack is when a cryptographic system is attacked, and the attacker has another source of information outputted by the system.

Timing Attacks

A timing attack can be possible if any of the following
depend on the contents of a secret:

Which instructions execute
Branching (if statements)
Memory access patterns

Notes:

There are many crazy forms of side channel attack, but the primary one is timing. Timing is also the only one that gets reliably sent back over a long distance.

An Example

Imagine this is the source code for a password checker:

#![allow(unused)]
fn main() {
fn verify_password(actual: &[u8], entered: &[u8]) -> bool {
 if actual.len() != entered.len() {
    return false;
 }

 for i in 0..actual.len() {
  if entered.get(i) != actual.get(i) {
   return false;
  }
 }
 true
}
}

What's the problem?

Notes:

Imagine you compile this into a little binary, and you are able to hit it repeatedly. When sending a guess into this, what information do you get back?

A boolean, and the amount of time from sending the password to getting back a response.

The problem is that the amount of time for a response reveals information about the password. An attacker can send in guesses repeatedly, and if it takes a longer amount of time to respond, that means more of the guess is correct.

Example (Cont)

What if we changed the code to look like this?

#![allow(unused)]
fn main() {
fn verify_password(actual: &[u8], entered: &[u8]) -> bool {
 actual == entered
}
}

Is this safe?

Notes: Now, we don't see any difference in the amount of lines of code or loops, right?

Example (Cont)

What does the source code look like?

#![allow(unused)]
fn main() {
// Use memcmp for bytewise equality when the types allow
impl<A, B> SlicePartialEq<B> for [A]
where
    A: BytewiseEq<B>,
{
    fn equal(&self, other: &[B]) -> bool {
        if self.len() != other.len() {
            return false;
        }

        // SAFETY: `self` and `other` are references and are thus guaranteed to be valid.
        // The two slices have been checked to have the same size above.
        unsafe {
            let size = mem::size_of_val(self);
            memcmp(self.as_ptr() as *const u8, other.as_ptr() as *const u8, size) == 0
        }
    }
}
}

Is this safe?

Notes:

Ok, still no. It looks like now the attacker can still figure out if the length of the password based on an early return. But what if we make sure all passwords are 16 bytes long. Now we are just using a single syscall. Is is safe then?

Example (Cont)

Let's check on memcmp.

memcmp(3) — Linux manual page

/* snip */

NOTES
       Do not use memcmp() to compare security critical data, such as
       cryptographic secrets, because the required CPU time depends on
       the number of equal bytes.  Instead, a function that performs
       comparisons in constant time is required.  Some operating systems
       provide such a function (e.g., NetBSD's consttime_memequal()),
       but no such function is specified in POSIX.  On Linux, it may be
       necessary to implement such a function oneself.

So how could we do it?

This is from the subtle crate, which provides constant time equality.

#![allow(unused)]
fn main() {
impl<T: ConstantTimeEq> ConstantTimeEq for [T] {
    /// Check whether two slices of `ConstantTimeEq` types are equal.
    ///
    /// # Note
    ///
    /// This function short-circuits if the lengths of the input slices
    /// are different.  Otherwise, it should execute in time independent
    /// of the slice contents.
    /* snip */
    #[inline]
    fn ct_eq(&self, _rhs: &[T]) -> Choice {
        let len = self.len();

        // Short-circuit on the *lengths* of the slices, not their
        // contents.
        if len != _rhs.len() {
            return Choice::from(0);
        }

        // This loop shouldn't be shortcircuitable, since the compiler
        // shouldn't be able to reason about the value of the `u8`
        // unwrapped from the `ct_eq` result.
        let mut x = 1u8;
        for (ai, bi) in self.iter().zip(_rhs.iter()) {
            x &= ai.ct_eq(bi).unwrap_u8();
        }

        x.into()
    }
}
}

Notes:

Now we've seen how hard it can be just to stop a very simple leak of timing information. Let's see what an actual cryptographic library concerns itself with.

Ed25519's Guarantees

This is an excerpt from the ed25519 description.

Foolproof session keys. Signatures are generated deterministically; key generation consumes new randomness but new signatures do not. This is not only a speed feature but also a security feature.
Collision resilience. Hash-function collisions do not break this system. This adds a layer of defense against the possibility of weakness in the selected hash function.

Ed25519's Guarantees (Cont.)

No secret array indices. The software never reads or writes data from secret addresses in RAM; the pattern of addresses is completely predictable. The software is therefore immune to cache-timing attacks, hyperthreading attacks, and other side-channel attacks that rely on leakage of addresses through the CPU cache.
No secret branch conditions. The software never performs conditional branches based on secret data; the pattern of jumps is completely predictable. The software is therefore immune to side-channel attacks that rely on leakage of information through the branch-prediction unit.

Takeway

Preventing side channel attacks is hard! Noticing sidechannel attacks is even harder!

DO NOT ROLL YOUR OWN CRYPTO

Notes:

Be very, very careful whenever you do anything that touches a secret. That includes any operation involving the secret, or reading/writing it somewhere.

When necessary, talk to a security expert or cryptographer.

Using Cryptographic Libraries Safely

Stay above the abstraction barrier
Validate each primitive's assumptions when combining primitives
Use the most reputable library you can
Realize when things need serious consideration
- Some potentially scary terms: Curve point, padding schemes, IV, twisted curve, pairings, ElGamal

Notes:

Reputableness of a library is some combination of:

used by many people
audited for security
reliable cryptographic literature
minimal external dependencies
recommended by cryptographers

If you get low-level enough in cryptography libraries to see these terms referenced in more than just a description, you're probably too low level.

Horror Stories

Notes:

Only go through a few of these based on interest and remaining time.

---v

PS3 Secret Key Leak

Problem: Bad randomness

Description: The ps3 developers didn't use randomness when signing with an algorithm that required randomness.

Consequence: Every PS3 was hardcoded to trust that key. When hackers got the key, they were then able to pretend to be Sony and write any software that ran on the PS3. In practice, it made running pirated games trivial.

Notes:

source

---v

IOTA's Novel Hash Function

Problem: Rolling your own crypto

Description: IOTA was a cryptocurrency with a value of 1.9B at the time. They wrote their own hash function, and researchers found severe vulnerabilities.

Consequence: Kind security researchers reported the flaw directly to devs. They had to pause the blockchain for 3 days, generate new address for all accounts, and swap to KECCAK.

Notes:

IOTA originally rolled their own hash function in an effort to be quantum-proof.

Some hash function weaknesses are weak. This was not. The proof of concept exploit literally found two hashes that correspond to a message for the blockchain sending a small amount of currency, and another that corresponded to a message sending a huge amount of money.

exploit POC shutdown source

---v

How the NSA wiretapped all cellphone calls for years

Problem: Small key space / secret technique

Description: The standard for cellphone calls up until the mid-late 2000s (GSM A5/1) used 54-bit keys, and the method was meant to be secret. It did not stay secret, and became extremely easily crackable.

Consequence: Intelligence agencies could and did easily wiretap calls. There were many brute-force attacks against the key space.

Notes:

When the standardization process started, professors proposed 128-bit keys. Western european (british especially) intelligence agencies wanted weaker security. Snowden eventually came out and said the NSA could easily read A5/1 calls.

article source source on weakening

---v

Why HTTPS isn't as secure as you'd hope

Problem: Cryptographic primitive assumptions not upheld

Description: Encryption does not generally hide the length of the underlying message. HTTPS often uses compression before encryption. The compression makes duplicated strings smaller.

Consequence: An exploit called BREACH can reveal a secret from an HTTPS-protected website in under 30 seconds. All websites have had to add mitigation to offset this attack.

Notes:

Mitigation looks like:

randomizing size of response content after compression
separating secrest from user input
disabling HTTP compression (this is expensive though)
randomizing secrets per request

source

Physical Security

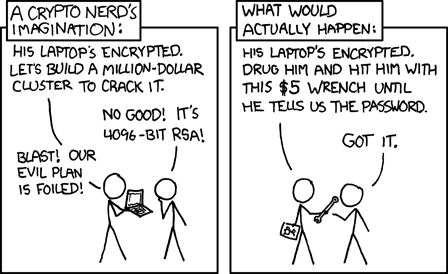
Notes:

Source is a classic XKCD comic.

Physical Security

Full physical access to a running computer can usually let an attacker have full access to your secrets with enough effort.

Some possible means:

Scanning all disk storage
Take out the RAM and swap it into a different computer to read (cold boot attack)
Proximate side-channel attacks
- RF emissions
- Power consumption
- Sound of a computer running

Notes:

Sources for exotic attacks:

HSMs

An HSM is a hardware security module. HSMs can make it much harder to impossible to steal cryptographic keys. An HSM will hold cryptographic keys, and perform operations on them.

Notes:

We don't go into this much, as there are many available resources around physical security and HSMs. This is just bringing up the ideas, in the context of what makes a cryptographic secret actually secret.

Security and Usability

The accessibility of a secret is typically inversely proportional to the security.

Making a secret more secure is often impractical, depending on the usage.

Notes:

This is not explicitly true in all cases, but it is a good rule of thumb. Additionally, note that impractical != impossible.