Hash Functions
How to use the slides - Full screen (new tab)
Hash Functions
Introduction
We often want a succinct representation of some data
with the expectation that we are referring to the same data.
A "fingerprint"
Hash Function Properties
- Accept unbounded size input
- Map to a bounded output
- Be fast to compute
- Be computable strictly one-way
(difficult to find a pre-image for a hash) - Resist pre-image attacks
(attacker controls one input) - Resist collisions
(attacker controls both inputs)
Hash Function API
A hash function should:
- Accept an unbounded input size (
[u8]byte array) - Return a fixed-length output (here, a 32 byte array).
#![allow(unused)] fn main() { fn hash(s: &[u8]) -> [u8; 32]; }
Example
Short input (5 bytes):
hash('hello') =
0x1c8aff950685c2ed4bc3174f3472287b56d9517b9c948127319a09a7a36deac8
Large input (1.2 MB):
hash(Harry_Potter_series_as_string) =
0xc4d194054f03dc7155ccb080f1e6d8519d9d6a83e916960de973c93231aca8f4
Input Sensitivity
Changing even 1 bit of a hash function completely scrambles the output.
hash('hello') =
0x1c8aff950685c2ed4bc3174f3472287b56d9517b9c948127319a09a7a36deac8
hash('hellp') =
0x7bc9c272894216442e0ad9df694c50b6a0e12f6f4b3d9267904239c63a7a0807
Rust Demo
Hashing a Message
Notes:
See the Jupyter notebook and/or HackMD cheat sheet for this lesson.
- Use a longer message
- Hash it
- Verify the signature on the hash
Speed
Some hash functions are designed to be slow.
These have applications like password hashing, which would slow down brute-force attackers.
For our purposes, we generally want them to be fast.
Famous Hash Algorithms
- xxHash a.k.a TwoX (non-cryptographic)
- MD5
- SHA1
- RIPEMD-160
- SHA2-256 (aka SHA256) &c.
- SHA3
- Keccak
- Blake2
xxHash64 is about 20x faster than Blake2.
Hash Functions in Blockchains
- Bitcoin: SHA2-256 & RIPMD-160
- Ethereum: Keccak-256 (though others supported via EVM)
- Polkadot: Blake2 & xxHash (though others supported via host functions)
Notes:
Substrate also implements traits that provide 160, 256, and 512 bit outputs for each hasher.
Exercise: Write your own benchmarking script that compares the performance of these algorithms with various input sizes.
Hashing Benchmarks
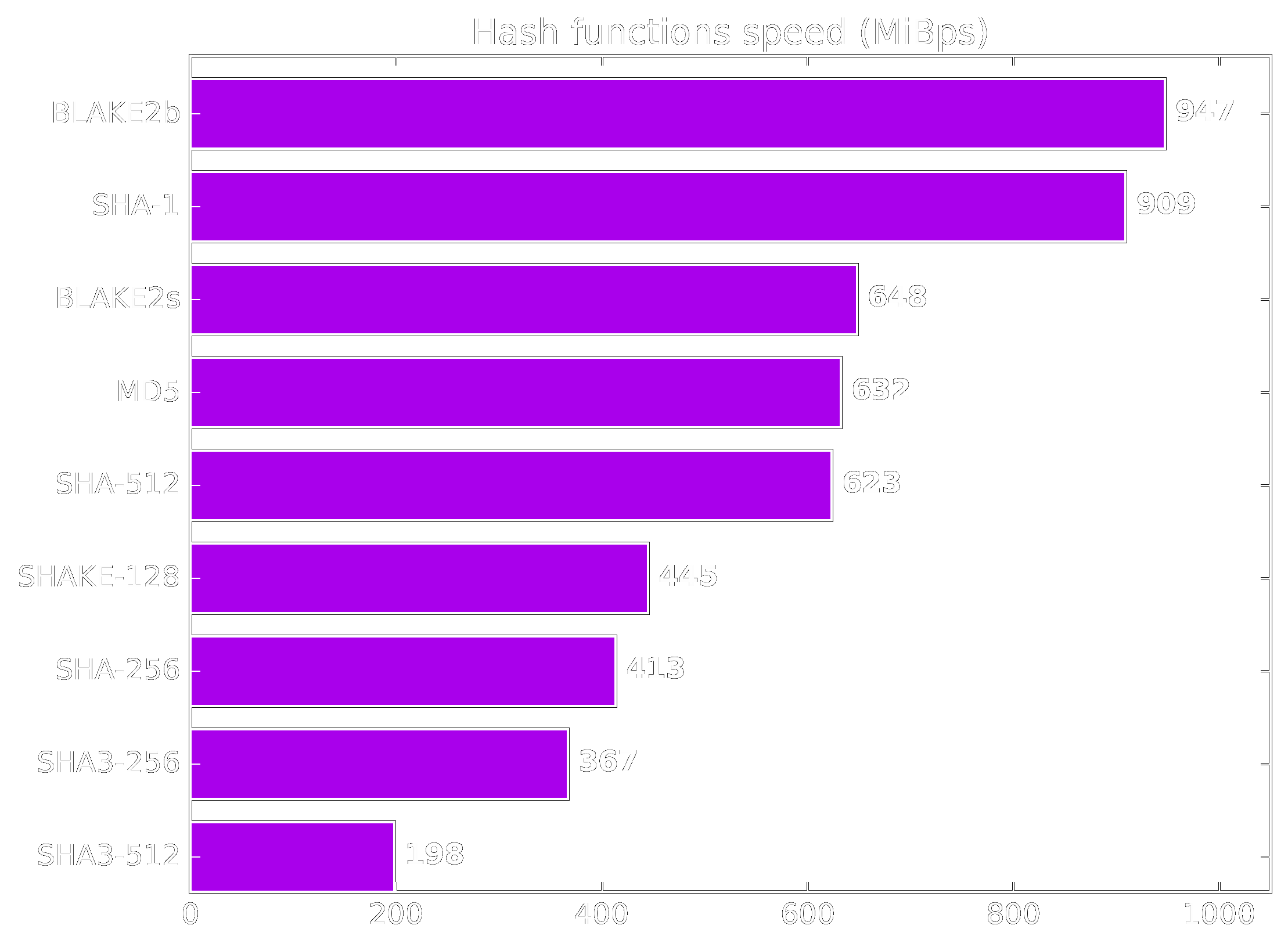
Notes:
Benchmarks for the cryptographic hashing algorithms. Source: https://www.blake2.net/
XXHash - Fast hashing algorithm
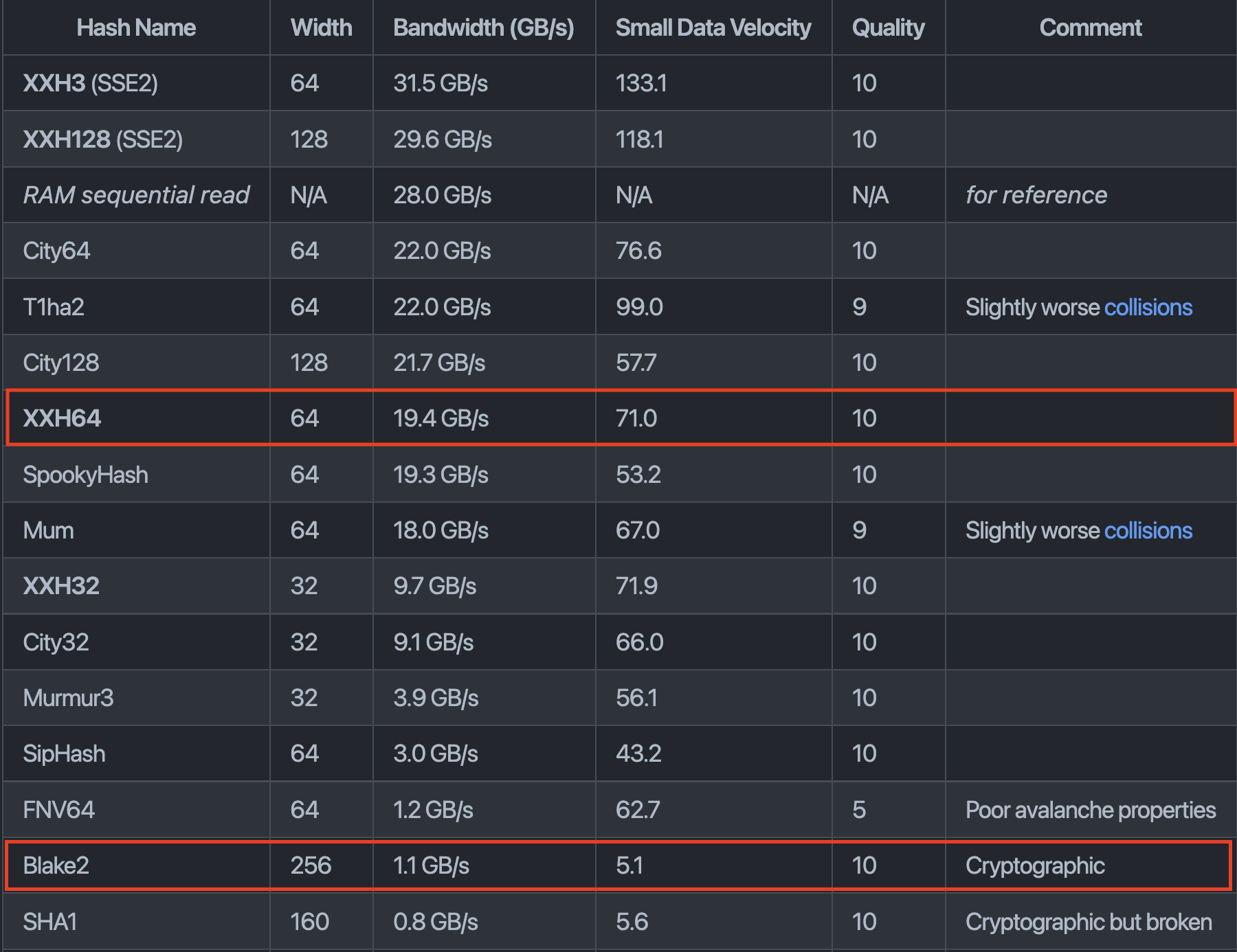
Notes:
Benchmarks for the XX-hash algorithms. Source: https://github.com/Cyan4973/xxHash#benchmarks
Non-Cryptographic Hash Functions
Non-cryptographic hash functions provide weaker
guarantees in exchange for performance.
They are OK to use when you know that the input is not malicious.
If in doubt, use a cryptographic hash function.
One Way
Given a hash, it should be difficult to find an input value (pre-image)
that would produce the given hash.
That is, given H(x), it should be difficult to find x.
Notes:
We sometimes add random bytes to pre-images to prevent guesses based on context (e.g., if you are hashing "rock, paper, scissors", then finding a pre-image is trivial without some added randomness.)
Second Pre-Image Attacks
Given a hash and a pre-image, it should be difficult to find another
pre-image that would produce the same hash.
Given H(x), it should be difficult to find any x'
such that H(x) == H(x').
Notes:
Since most signature schemes perform some internal hashing, this second pre-image would also pass signature verification.
Collision Resistance
It should be difficult for someone to find two messages that
hash to the same value.
It should be difficult to find an x and y
such that H(x) == H(y).
Collision Resistance
Difference from second pre-image attack:
In a second pre-image attack, the attacker only controls one input.
In a collision, the attacker controls both inputs.
They may attempt to trick someone into signing one message.
Notes:
Attacker has intention to impersonate the signer with the other. Generally speaking, even finding a single hash collision often results in the hash function being considered unsafe.
Birthday Problem
With 23 people, there is a 6% chance that someone will be born on a specific date, but a 50% chance that two share a birthday.
- Must compare each output with every other, not with a single one.
- Number of possible "hits" increases exponentially for more attempts, reducing the expected success to the square-root of what a specific target would be.

Birthday Attack
Thus, with a birthday attack, it is possible to find a collision of a hash function in $\sqrt {2^{n}}=2^{^{\frac{n}{2}}}$, with $\cdot 2^{^{\frac{n}{2}}}$ being the classical preimage resistance security.
So, hash function security is only half of the bit space.
Notes:
e.g., a 256 bit hash output yields 2^128 security
Partial Resistance
It should be difficult for someone to partially (for a substring of the hash output) find a collision or "second" pre-image.
- Bitcoin PoW is a partial pre-image attack.
- Prefix/suffix pre-image attack resistance reduces opportunity for UI attacks for address spoofing.
- Prefix collision resistance important to rationalize costs for some cryptographic data structures.
Hash Function Selection
When users (i.e. attackers) have control of the input, cryptographic hash functions must be used.
When input is not controllable (e.g. a system-assigned index), a non-cryptographic hash function can be used and is faster.
Notes:
Only safe when the users cannot select the pre-image, e.g. a system-assigned index.
Keccak is available for Ethereum compatibility.
Applications
Cryptographic Guarantees
Let's see which cryptographic properties apply to hashes.
---v
Confidentiality
Sending or publically posting a hash of some data $D$ keeps $D$ confidential, as only those who already knew $D$ recognize $H(D)$ as representing $D$.
Both cryptographic and non-cryptographic hashes work for this. only if the input space is large enough.
---v
Confidentiality Bad Example
Imagine playing rock, paper, scissors by posting hashes and then revealing. However, if the message is either "rock", "paper", or "scissors", the output will always be either:
hash('rock') = 0x10977e4d68108d418408bc9310b60fc6d0a750c63ccef42cfb0ead23ab73d102
hash('paper') = 0xea923ca2cdda6b54f4fb2bf6a063e5a59a6369ca4c4ae2c4ce02a147b3036a21
hash('scissors') = 0x389a2d4e358d901bfdf22245f32b4b0a401cc16a4b92155a2ee5da98273dad9a
The other player doesn't need to undo the hash function to know what you played!
Notes:
The data space has to be sufficiently large. Adding some randomness to input of the hash fixes this. Add x bits of randomness to make it x bits of security on that hash.
---v
Authenticity
Anyone can make a hash, so hashes provide no authenticity guarantees.
---v
Integrity
A hash changes if the data changes, so it does provide integrity.
---v
Non-Repudiation
Hashes on their own cannot provide authenticity, and as such cannot provide non-repudiation.
However, if used in another cryptographic primitive that does provide non-repudiation, $H(D)$ provides the same non-repudation as $D$ itself.
Notes:
This is key in digital signatures. However, it's important to realize that if $D$ is kept secret, $H(D)$ is basically meaningless.
Content-Derived Indexing
Hash functions can be used to generate deterministic
and unique lookup keys for databases.
Notes:
Given some fixed property, like an ID and other metadata the user knows beforehand, they can always find the database entry with all of the content they are looking for.
Data Integrity Checks
Members of a peer-to-peer network may host and share
file chunks rather than large files.
In Bittorrent, each file chunk is hash identified so peers can
request and verify the chunk is a member of the larger,
content addressed file.
Notes:
The hash of the large file can also serve as a signal to the protocol that transmission is complete.
Account Abstractions
Public keys can be used to authorize actions by signing of instructions.
The properties of hash functions allow other kinds of representations.
Public Key Representation
Because hashes serve as unique representations of other data,
that other data could include public keys.
A system can map a plurality of key sizes to a fixed length
(e.g. for use as a database key).
For example, the ECDSA public key is 33 bytes:
Public key (hex):
0x02d82cdc83a966aaabf660c4496021918466e61455d2bc403c34bde8148b227d7a
Hash of pub key:
0x8fea32b38ed87b4739378aa48f73ea5d0333b973ee72c5cb7578b143f82cf7e9
^^
Commitment Schemes
It is often useful to commit to some information
without storing or revealing it:
- A prediction market would want to reveal predictions only after the confirming/refuting event occurred.
- Users of a system may want to discuss proposals without storing the proposal on the system.
However, participants should not be able to modify their predictions or proposals.
Commit-Reveal
- Share a hash of data as a commitment ($c$)
- Reveal the data itself ($d$)
It is normal to add some randomness to the message
to expand the input set size:
$$ hash(message + randomness) => commitment $$
Commitment: 0x97c9b8d5019e51b227b7a13cd2c753cae2df9d3b435e4122787aff968e666b0b
Reveal
Message with some added randomness:
"I predict Boris Johnson will resign on 7 July 2022. facc8d3303c61ec1808f00ba612c680f"
Data Identifiers
Sometimes people want to store information in one place and reference it in another. For reference, they need some "fingerprint" or digest.
As an example, they may vote on executing some privileged instructions within the system.
The hash of the information can succinctly represent the information and commit its creator to not altering it.
Data Structures (in Brief)
This is the focus of a later lesson.
Notes: For now, just a brief introduction.
Pointer-Based Linked Lists
Pointer-based linked lists are a foundation of programming.
But pointers are independent from the data they reference,
so the data can be modified while maintaining the list.
That is, pointer-based linked lists are not tamper evident.

Hash-Based Linked Lists
Hash-based lists make the reference related to the data they are referencing.
The properties of hash functions make them a good choice for this application.
Any change at any point in the list would create downstream changes to all hashes.
Merkle Trees
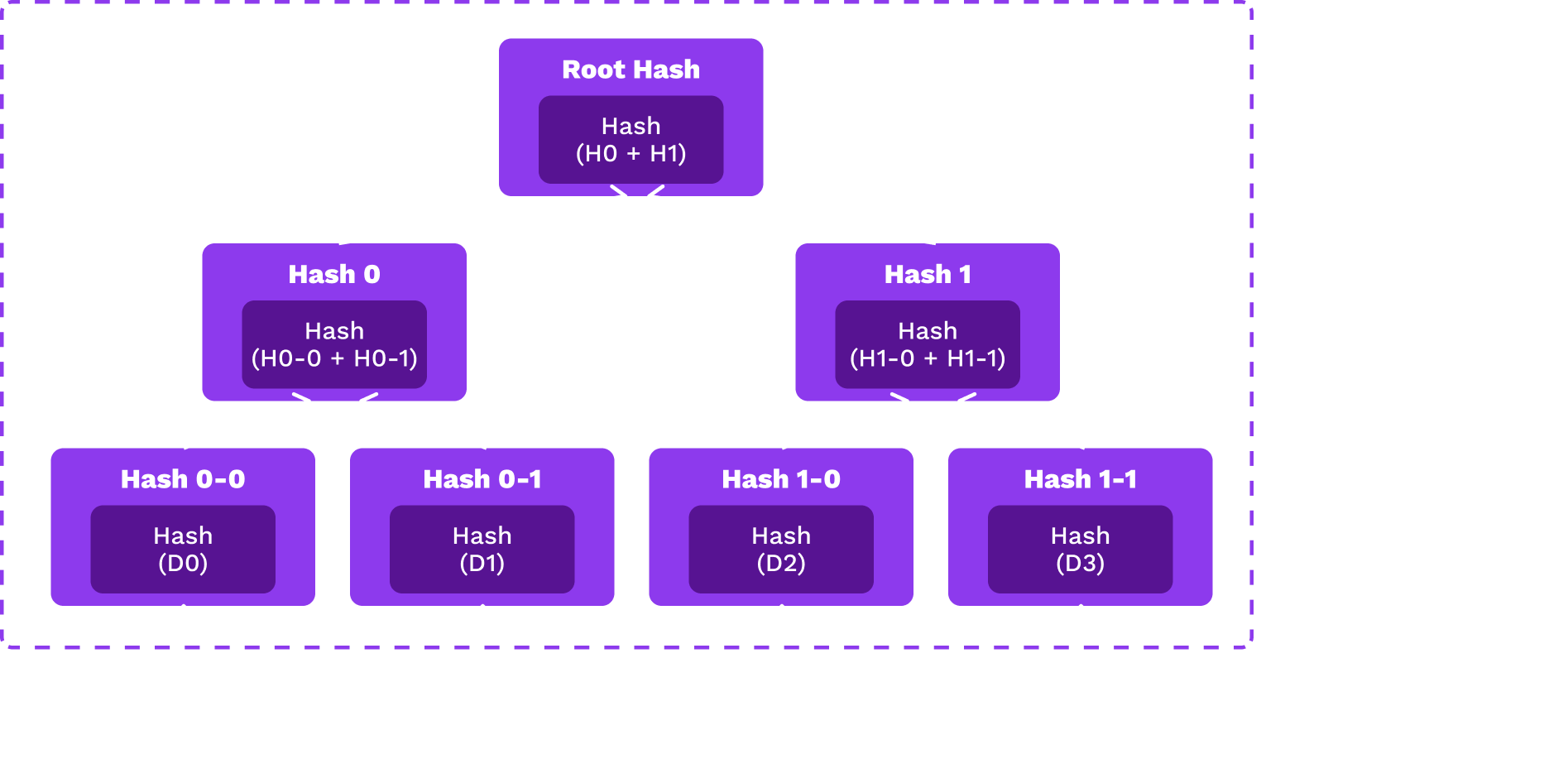
Notes:
Each leaf is the hash of some data object and each node is the hash of its children.
Proofs
Merkle trees allow many proofs relevant to the rest of this course,
e.g. that some data object is a member of the tree
without passing the entire tree.
More info in the next lesson.
Questions
Hash Examples in Substrate
Sr25519 Signatures
Sr25519 hashes the message as part of its signing process.
Transactions
In transactions in Substrate, key holders sign a
hash of the instructions when the instructions
are longer than 256 bytes.
Database Keys
TwoX64 is safe to use when users (read: attackers)
cannot control the input, e.g. when a
database key is a system-assigned index.
Blake2 should be used for everything else.
Again, there is a whole lesson on hash-based data structures.
Other Uses of Hashes in Substrate
Hashes are also used for:
- Generating multisig accounts
- Generating system-controlled accounts
- Generating proxy-controlled accounts
- Representing proposals
- Representing claims (e.g. the asset trap)