Price Finding Mechanisms

Price Finding Mechanisms

Introduction

• A central topic of economics is price finding in markets.
• How does a buyer and a seller agree on the price of a good?

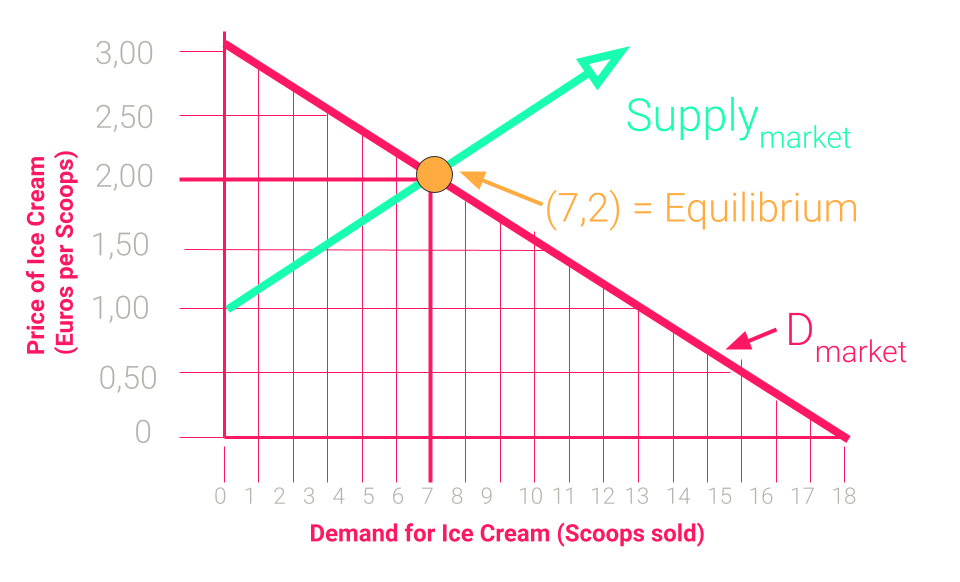
Supply / demand for BIG markets

Notes:

• As we saw yesterday, a market price must balance supply and demand.
• Demand: number of items bought by consumers at a given price.
• Supply: number of items produced and sold at a given price.

Supply-demand for BIG markets

• Supply-demand model works well for big markets.
• We have lots of buyers, sellers, lots of info.
• Predictable market price, balancing supply and demand.
• Only sensible price at which a buyer and seller can trade.

Notes:

• When a particular good has a large number of buyers and sellers, and we have a well established market with lots of real-life trading data, we can develop a supply-demand model.
• It allows us to accurately predict the price at which the market will converge to for a good, which is the point at which supply and demand balance out.
• It only makes sense to trade at market price: if lower, the seller can easily find another buyer willing to pay more, if higher, the buyer can easily find another seller willing to charge less.

What about difficult markets?

Notes:

Image source: https://funkypriceguide.com/collectible/512-gold-hopper-2018-sdcc-fundays/

What about difficult markets?

Today we focus on markets with few buyers or sellers, few trades, or non-standardized goods.

Notes:

• The supply-demand model does not work in these examples
• First example: there is a single buyer
• Second example: very few buyers and sellers, trades are very infrequent, and goods are not standardized
• Third example: not enough public data about the good.
• In second and third cases, buyers may have wildly different personal valuations of the good.
• A standardized good could be a liter of milk. A less standardized good is a wedding ring, or a painting

A simple model

How does Selena optimally sell the item?

Notes:

• We consider the limit case of one single seller and two buyers, to keep things simple.
• Throughout the talk we assume that a buyer will purchase the item if the price is below or equal to their valuation.

Let's assume...

Notes:

• We saw the notion of an abstraction already in game theory class: we lose a bit in realism, but gain in structure which allows us to make precise statements, and develop a richer theory. The intuition and conclusions still apply in real life.
• In particular, we are assuming that each of the three characters has a certain amount of information about the valuations of the other players, namely the distribution they are sampled from, and they can use this info to strategize their actions.
• Assuming that each valuation $v_i$ follows a uniform distribution between 0 and 1 simplifies Selena's life, because she knows that for any value $x\in [0,1]$, the probability that a bidder's valuation is below $x$ is exactly $x$, i.e., $P[v_i\leq x]=x$.
• However, assuming a uniform distribution is just for pedagogical reasons: most results in auction theory can be extended to more general distributions.

Price posting

• Simplest solution: Selena posts a price $p$, sells item to first taker.
• What is her optimal price $p$? One maximizing her expected revenue.
• Expected revenue: price $\times$ prob. of making a sale.
• For price $p$, prob. of making a sale is $(1-p^2)$.
• Hence her expected revenue is $p \cdot ( 1-p^2)$.

Notes:

• If both buyers accept the posted price, we assume the firm selects a random buyer to trade with.

• The proof of this and all other math formulas can be found in the slides, for anyone interested.

• Assuming that 100% of the sale price is profit for the seller, this profit is

  • $p$ in case of selling, $0$ otherwise, where
  • $(1-p^2)$ is the probability of selling the item.
  • To see this probability, consider conversely that the probability that none of the buyers accepts the price must be $p^2$, because each valuation must be below $p$, and these are two individual events each happening with probability $p$ (recall: valuations are uniformly distributed between 0 and 1).

• $Pr{v_i \leq x}$ is the probability that the randomly drawn value of valuation $v_i$ is below $x$.

• Independent values will be important: when is this (not) a sensible assumption? (Example: oil drilling rights auctions, ...)

• Uniform distribution is just for pedagogical reasons; standard model allows for more general distributions.

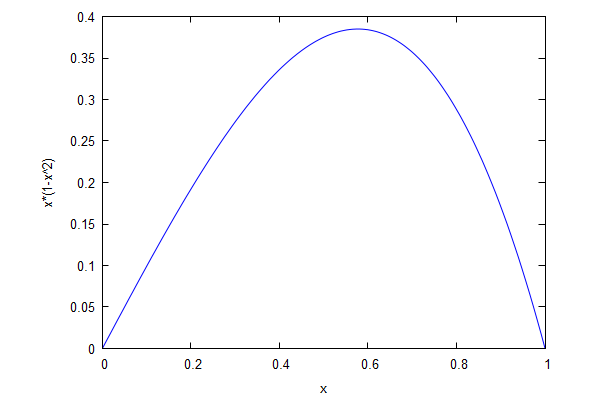
Price posting

• At the optimum point, expected revenue is $\approx 0.38$.
• We will see that an auction can do better.

Notes:

• Prices, valuations, and revenue are given in the same currency unit, say, USD.
• How do we maximize the expected revenue function $f(p)=p ( 1-p^2)$? The function has a unique peak, so at the maximum, the first derivative must be zero.
• The function is maximized for a $p$ satisfying $$ f'(p)=1-p^2 - 2p^2 = 0 \implies p = \sqrt{1/3}.$$
• Expected revenue is then $f(\sqrt{1/3})=\frac{2}{3}\sqrt{1/3}\approx 0.38.$

Auctions

Lesson summary

Notes:

• Auctions can provide more revenue to the seller, as we will see.
• In a market with a posted price, buyers never need to reveal their valuation (i.e., how much they would actually be willing to pay for an item). In auctions, the same is generally true, as they may bid values much lower than their valuations, but there is an auction format where they tend to bid their actual valuations (called truthful bidding).
• There is a specific sense in which, in theory, all four auction formats provide the same revenue for Selena.
• However, in practice, some formats may be better suited than others, and we will see some such examples.

Auctions

• Alice and Bob (bidders) submit bids based on own valuations.
• Selena (auctioneer) selects winner to allocate the item to.
• The winner's payment is a function of the bids.

An auction is a competitive game for buyers, where the seller makes the rules.

Notes:

• Bidders submit bids to auctioneer, which are a declaration of how much they are willing to pay for the item. In an ideal world, a bid equals the bidder's valuation (this is called a truthful bid), but of course depending on the bidder's strategy they may choose to underbid or overbid.
• In this lesson we will have some fun analyzing the bidders' best strategies as well as the auctioneer's best strategies.
• Both the winner and the winner's payment will dependent on the bids and the auction rules. The payment cannot be higher than the winner's bid, but it could be lower.
• Auctions yield a higher revenue because they create competition among buyers.

Auction formats

Notes:

• In static auctions, bidders give their bids simultaneously and cannot change it later.
• Static auctions are also called sealed-bid auctions, as many times in practice the bids are submitted in sealed envelopes to the auctioneer.

Auction formats

Four auction formats we discuss today:

Notes:

• Example, Selena auctions off a painting. Suppose in a static auction, Alice bids 1000 and Bob bids 2000. In a first-price format, Bob wins and pays 2000. In a second-price format, Bob still wins but only pays 1000.
• The English format became popular in England. Selena continuously raises the price as long as at least 2 bidders accept it. As soon as only one bidder remains, they win and pay the current price.
• The Dutch format became popular in the Netherlands, particularly in the tulip market. Selena starts at a high price and continuously lowers it as long as there are no takers. As soon as a bidder accepts the price, they win and pay the current price.
• We are gonna analyze each of these four formats, and take the opportunity to discuss relevant notions in auction theory along the way.
• For me, the second-price auction is the least intuitive format. But it turns out to be one of the nicest and easiest to analyze, so we will start there.

Second-price auction

• Why make the winner pay the second highest bid?
• Least intuitive format, but strategically simplest for bidders.
• Simply bid your valuation truthfully!
• A bidder wants to maximize their expected profit:
  • own valuation - price paid, in case they win
  • zero, otherwise

Notes:

• Out of the four formats, we start our analysis with second-price static auctions, i.e., Alice and Bob give their bids in sealed envelopes to Selena, and she declares the winner to be the one with the highest bid, but the price to pay is only second highest bid.
• To analyze the bidders' best strategy, we assume that each bidder wants to maximize their expected profit. Again, this is a sensible but strong assumption, as they could have some other equally sensible objectives. By the end of the lesson we will highlight how this assumption can be a bit unrealistic in practice.

Second-price auction

• Truthful equilibrium: a dominant strategy to bid truthfully.
• Dominant strategy: outcome is at least as good as the outcome of any other strategy, no matter what the other bidder bids.

Notes:

• We can immediately say that you should never overbid (i.e., bid above your valuation), because in that case your profit can only be zero (if you lose) or negative (if you win). So the key question is whether you should ever underbid.
• In the case that Bob's bid is higher than your valuation, bidding truthfully or underbidding both lead to losing and having a revenue of zero.
• But if Bob's bid is lower than your valuation, any bid between these two values leads to you winning and having the same profit (namely the difference of these values), hence there is no gain in underbidding. However if you underbid too much, you run the risk of losing and having zero profit.
• Hence in both cases we see that underbidding does not increase your profit, and can only decrease your chance of winning. So it is better to bid exactly your valuation.
• The proof can be easily generalized to any number of bidders (to obtain that in a second-price auction, it is a dominant strategy for each bidder to bid truthfully.

TIP: use arrow chars in unicode for style: https://www.htmlsymbols.xyz/arrow-symbols

Second-price auction

Expected revenue

• Selena's expected revenue is expected value of 2nd highest valuation.
• For two independent variables uniformly sampled from $[0,1]$, the expected value of the minimum is $1/3\approx 0.33$.
• This is not quite as good as posting a price (which provided expected revenue $0.38$). Why not?

Notes:

• Let $F(x)$ be the cumulative density function (CDF) of the lowest of Alice and Bob's valuations, $\min{v_A, v_B}$, where $v_A$ and $v_B$ are independent variables sampled uniformly from $[0,1]$.
• By definition, for any $x$ in $[0,1]$, $F(x)$ is the probability that the lower valuation is below $x$, or equivalently, $g(x):=1-F(x)$ is the probability that both valuations are above $x$; clearly $g(x)=(1-x)^2$, and hence $F(x)=1-(1-x)^2$.
• From the CDF, we can compute the probability density function (PDF) by derivation: $f(x)=\frac{d}{dx}F(x)=2(1-x)$.
• Finally, the expected value is computed from the PDF with the integral formula $$\int_0^1 x\cdot f(x) dx = 2\int_0^1 (x-x^2)dx=2\cdot \left(\frac{1}{2}-\frac{1}{3}\right)=\frac{1}{3}.$$

Reserve price

• Because the format we considered is not optimal for the auctioneer!
• The optimal auction involves a reserve price $r>0$:
  • If no bid is above $r$, nobody wins.
  • If one bid is above $r$, the payment is $r$.
  • If both bids are above $r$, the payment is the second-highest bid.

Reserve price

Fact: Under any reserve price $r$, it is still optimal to bid truthfully, and if Selena sets $r=0.5$, her expected revenue is $\approx 0.42$, so it is better than posted price (where expected revenue was $\approx 0.38$).

Reserve price

Notes:

• The proof idea is that if $r=0.5$, half of the time one valuation is above it and the other is below it, and the reserve price increases the paying price. On the other hand, if both valuations are below $r$ then there is no sale, which decreases Selena's revenue, but this case only happens one quarter of the time. Finally, if both valuations are above $r$, the presence of a reserve price does no affect the result. Overall, there is a positive net gain in Selena's expected revenue. Below we present the formal proof.
• The probability that both valuations are below $r$ is $r^2$, the prob. that $r$ is in between the valuations is $2r(1-r)$, and the prob.that both valuations are above $r$ is $(1-r)^2$. You can check that these probabilities sum up to one.
• In the first case Selena's revenue is zero, and in the second case it is $r$. Hence the expected revenue for the first two cases is $2r^2(1-r)$.
• To compute the expected revenue of the third case, we simply copy the integral formula for the expected value (from a couple of slides ago), but we restrict the integration limits to $[r, 1\]$: \begin{align} \int_r^1 x\cdot f(x) dx &= 2\int_r^1 (x-x^2)dx\ &=2\cdot \left[\frac{x^2}{2}-\frac{x^3} {3}\right\]_r^1 \&=\frac{1}{3} - r^2 + \frac{2}{3}r^3. \end{align}
• Putting all terms together, we obtain that the expected revenue is $$R(r)=0+2r^2(1-r)+\left(\frac{1}{3} - r^2 + \frac{2}{3}r^3\right)=\frac{1}{3}+r^2-\frac{4}{3}r^3.$$
• To maximize the auctioneer's expected revenue function $R(r)$ above:
  • We evaluate the function at all the local extrema (minima and maxima).
  • Since the function is continuous and differentiable, the local extrema are found at the borders $r=0$ and $r=1$, and at the roots of the derivative $R'(r)=2r-4r^2=0$. These roots are $r=0$ and $r=1/2$.
  • By inspecting all these points, we find that the global maximum is found at $r=1/2$, with a value of $R(1/2)=5/12\approx 0.42$.
• Literature: Myerson, Roger B. "Optimal auction design." Mathematics of Operations Research 6, No. 1 (1981): 58-73.

English auction

Recall the rules:

Notes:

• Next we move to English auctions, which have a very similar analysis.
• Notice it has a flavor of a second-price auction: the price you pay is decided by another bidder, not you.
• In a sense, these two auction formats are strategically equivalent!

English auction

• English auction is strategically equivalent to static second-price auction.
• It is a dominant strategy to stay until the price reaches one's valuation.
• The expected revenue for Selena is the also the same!
• Consequently, these two formats are also revenue equivalent.

Notes:

• Why is staying until the price reaches your valuation a dominant strategy?
  • If you leave you get zero utility.
  • If you stay while the price is below your valuation, your eventual utility may be zero or positive, so there is no incentive to leave.
  • If you stay while the price is above your valuation, your utility is zero or negative, so you should leave immediately.

Shill bidding

• Second-price and English auctions popular among theorists, not so popular among practitioners.
• One reason is that they are prone to shill-bidding: bidder that acts on behalf of the auctioneer to drive up the price.

Notes:

• Both second-price auctions and English auctions have the truthful bidding property, which is very satisfactory for theorists. However, as you can probably tell, they are not so popular in practice.
• A shill bidder has no intention of winning, but just increasing the price that the winner must pay. They do it to benefit the auctioneer.
• Shill bidding is frowned upon, sometimes illegal, but it is usually hard or impossible to prove and to prevent.

First-price auction

Notes:

• New topic, time to wake up!
• We move on to first-price auction, which as you recall, is a type of sealed auction.
• Its analysis is more involved, and the resulting optimal bidding strategy is quite different from before.

First-price auction

Bidding in the first-price auction is not truthful.

• Bidding truthfully can never be optimal: if you win, you earn nothing.
• Underbidding is strictly better, you win sometimes and when you do you have a positive utility.

First-price auction

Equilibrium strategy: It is a Nash equilibrium for each bidder to bid half their own valuation.

Nash equilibrium: A set of strategies, one per player, where no one has an incentive to change their strategy.

Notes:

• Recall Nash equilibrium we already covered.
• A Nash equilibrium is a "recommended strategy per player", such that if you assume that the other bidder will follow their recommendation, then the best you can do is to follow yours.
• As the same is true for the other players, it is indeed a reasonable assumption to think the other players will follow their recommendation.
• However, if the other players picks an unexpected strategy, your recommended strategy may be suboptimal. In this sense, a Nash equilibrium is a weaker concept than a dominant strategy, in which the strategy of the other players is irrelevant.

First-price auction

Intuition: suppose you are Alice

• If you bid 0, winning prob. is zero.
• If you bid your valuation, profit is zero.
• Hence, there is a sweet spot between 0 and your valuation where your expected profit is maximal.
• It turns out this is bidding half your valuation, at which point you and Bob each wins half of the time.

Notes:

• Unfortunately, the full proof is outside the scope of the presentation, but we provide it here in the lesson notes.
• Assume you are Alice, with valuation $v_A$ and bid $b_A$.
• Assuming that Bob's bid $b_B$ equals half his valuation $v_B$, that $v_B$ is sampled uniformly at random between 0 and 1, and that your bid $b_A$ is at most $1/2$, your winning probability is: \begin{align} Pr[winning] &= Pr[b_B\leq b_A] \ &= Pr[v_B/2 \leq b_A] \ &= Pr[v_B \leq 2b_A] \ &= 2b_A. \end{align}
• Your profit in case of winning is $(v_A-b_A)$, hence your expected profit is $2b_A(v_A-b_A)$.
• It can be checked that this expression is maximized for $b_A=v_A/2$.
• In summary, if Bob bids half his valuation, it is optimal for Alice to bid has her valuation, and vice versa. Together we have a Nash equilibrium.

First-price auction

Expected revenue

• Reasonable to assume each bidder bids half their valuation.
• Hence, Selena's revenue is $\frac{1}{2}\max{v_A, v_B}$.
• The expected value of $\max{v_A, v_B}$ is $2/3$.
• Hence, her expected revenue is $1/3$.

The same as in second-price auction!

Notes:

• I find this result fascinating. The optimal strategies are so different, but somehow the fact that you underbid is exactly compensated by the fact that you pay more when you win.
• Is there a deeper connection going on here? Or is it just a coincidence that the expected revenues are all the same so far?
• Formal proof of the expected revenue: recall that the valuations $v_A$ and $v_B$ are assumed to be independent variables uniformly drawn from $[0,1]$.
• The cumulative density function (CDF) of the higher valuation, $\max{v_A, v_B}$, is $F(x)=x^2$. This is because $F(x)$ is lower than $x$ only if both valuations are below $x$, and these are two independent events each happening with probability $x$.
• Then, the probability density function (PDF) is $f(x)=F'(x)=2x$.
• And the formula for the expected value of $\max{v_A, v_B}$ is $$R = \int\limits_0^1 x\cdot f(x)\mathrm d x = \int\limits_0^1 2x^2 \mathrm d v = \frac{2}{3}.$$

Revenue Equivalence

Fact: When valuations are secret and independent, there is no reserve price, and item goes to highest bidder, then all auction mechanisms are revenue equivalent.

Notes:

• This is a theorem established by Myerson in 1981.
• Notice all auction formats are not strategically equivalent (namely, you should bid truthfully in some formats but not in others), yet they are still revenue equivalent for the auctioneer.
• This result is very surprising to me, and one of the coolest results in game theory.

Dutch auctions

Notes:

• We finally say a few words about the fourth and last auction format.
• Notice it has a flavor of a first-price auction: you pick the price you pay. So you definitely do not want to bid truthfully, but rather underbid.

Dutch Auction

Recall the rules:

• The auctioneer continually lowers the price.
• At any price, you can decide whether or not to accept the price.
• If you are the first to accept the price, you win and pay the price you just accepted.

Dutch Auction

• It turns out that the Dutch auction is strategically equivalent and revenue equivalent to the static first-price auction.
• The price that you accept in the Dutch auction corresponds to the price that you'd bid in a static first-price auction.
• The tradeoffs that the bidders face are very similar: take the current price or wait a bit at the risk of another bidder accepting first. It is an equilibrium to wait till the price is half your valuation.

Recap

Break (10 minutes)

Discussion

Independence of valuations

In our analysis, it was important to assume that bidders' valuations are independent from one another.

Can you think of examples where this assumption isn't sensible?

Independence of valuations

Answer:

Sensible: - a piece of art, where the bidders are final clients.

Not sensible: drilling rights to an oil well. Bidders will have similar estimates of amount of oil, hence valuations are highly correlated.

Common value auctions

Special scenario: there is a unique valuation of item, but each bidder only has a private estimate of it.

In these cases, it is observed that sealed-bid auctions tend to give higher revenue than dynamic auctions.

Why do you think this is the case?

Common value auctions

The auction may be used as a means of gathering information from other participants to triangulate a price

Answer: In a dynamic auction, a bidder can use the bids of others as additional signals of the correct valuation. If bids so far seem high, my initial estimate must be low, and vice versa, so I can adjust my personal estimate. Hence estimates converge.

In a static auction, there is no convergence of estimates, so it is more likely that some bidders keep unusually high estimates. As a result, there is a higher chance that the winner ends up paying more than the correct valuation. This is known as the winner's curse.

Equivalence of revenues

It is observed in practice that first-price auctions lead to higher revenue than second-price auctions.

This violates the equivalence of revenues, so an assumption in our analysis fails consistently.

What do you think it is?

Equivalence of revenues

Answer: Risk aversion. People prefer lower uncertainty games, even if this means lower expected profits.

Would you rather win a million dollars with a 50% chance, or 300 thousand with a 90% chance?

In Nash equilibrium analysis for first-price auctions, we claimed that if Bob bids half his valuation, then Alice should bid half hers, so each wins 50% of time. But we implicitly assumed that Alice is risk neutral. Yet she might prefer to bid more and win more often.

Notes:

• Of course, Bob may react the same way and also bid more in an attempt to bid more often. As a result, they may still win about 50% of the time each, but both end up bidding too much due to their risk aversion.
• In contrast, in our analysis for second-price auctions, the bidders' aversion to risk is not a factor.
• Important: If you want to maximize the auctioneer's revenue and don't mind playing psychological games with the bidders, you should choose first price auctions over second-price auctions.

Front Running

Computer systems may have front runners: special nodes can see an incoming bid, react by creating their own bid, and make it look like their bid was created first.

If you run an auction on a system with front runners, which of the four auctions would you use? Why?

Notes:

• Front runners are a known problem in eBay, trading platforms, and blockchain networks, etc.
• Front runners have a special, faster setup that allows them to see an incoming message from a bidder, react to it by creating their own message, and make their message get registered first in the system.

Front Running

Answer: Meet front runner Fred.

In a Dutch auction, if Fred is a bidder he waits for first bidder to signal accepting the price, and Fred makes the signal first. He's guaranteed to win with least possible price.

In second-price auction, if Fred is auctioneer he can shill bid successfully: when a highest bid arrives, he creates bid slightly under it and makes it appear as if it was created first.

Front Running

Answer: Meet front runner Fred.

In a first-price auction, if Fred is bidder and if he can "open the seals" he can win by slightly outbidding highest bid. (Poor data privacy, a common issue in computer systems)

Hence, it might be best to run an English auction.

Sniping

In a dynamic auction with a fixed bidding time window, sniping is placing a highest bid as late as possible, so other bidders can't react and overbid you. The practice leads to low revenue. Particularly bad when done by a front runner (microseconds).

How to protect an auction from snipers?

Notes:

• eBay uses such types of auctions, and is infamous for having snipers.

Sniping

Answer: candle auctions.
Dynamic first-price auction with random ending time.

Sniping

Answer: candle auctions.
Dynamic first-price auction with random ending time.

• Similar to first-price auction
• except that ending time is unpredictable.
• At ending time, current highest bidder wins, pays own bid.
• Sniping protection: the longer you wait to bid, the higher the chances the auction ends.

Notes:

• Fun fact: candle auctions were popular in England in the 17th and 18th centuries.
• They would use a candle (hence the name). When the flame extinguishes, the auction is over.
• Fun fact: Polkadot implemented a candle auction for assigning block space to applications.

Workshop: Auction Games

NFT Auction

• You have the chance to bid on one of 25 unique NFTs that are created by a professional artist.
• Use your budget that you accumulated during the last Academy Games.
• Everything that you will not use for bidding (or if your bid was lower than your budget), you will receive in cash at the end of the Academy.
• 100% of the revenue of the auctions goes to the artist.
• You are randomly assigned to one of three auction formats

The Artist & NFTs!

Jeremy Gluck (Nonceptualism)

• Canadian Artist living in Great Britain.
• Diverse Practice: Post-digital fine art in NFT, digital art, film, photography, sound and video art, installation, and performance.
• Exhibitions: Works showcased offline in cities like London, Sydney, Bath, Anglesey, and Swansea, and online in various publications.
• Art is exhibited in Tides Fine Art Gallery, Mumbles, Wales.

Format 1: Activity Rule Auction

• The initial bidding phase lasts 30 seconds.
• Every valid bid resets the timer.
• You need to bid at least 30 cents more than the previous highest bid.
• Whoever has the highest bid at the end, wins. Winners pay their bids.

Format 2: Candle Auction

• Auction Format from the 16th Century.
• The auction lasts for exactly 4 minutes.
• A “candle mechanism” randomly determines, after the auction, when the auction ended
• Grace-period of 1 minute.
• Candle Phase of 3 minutes.
• Whoever had the highest bid when the auction actually ended, wins.

Format 3: Hard Close Auction

• Similar to eBay auctions.
• Auction lasts for 4 minutes.
• Whoever has the highest bid at the end of the auction, wins.
• Winners pay their bids.

Auction 2: Questions?

Auction 2: NFT Auction

Link will be distributed!

Auction 2: Discussion

Auction 2: Results!

Further Reading

Polkadot & Kusama Auctions
Data & Background information:

Questions

Bonus Game: Dollar Auction

Notes:

• Thought experiment designed by economist Martin Shubik.
• Serves as analogy for war: it may be apparent for both sides that even winning the war won't make up for the losses, yet both sides are motivated to keep spending money on it.
• You could get 1 dollar for 5 cents if no one else bids.
• But if you end up second you have a loss.

Dollar Auction: Questions?

Dollar Auction

Discussion

• Would you consider the auction paradoxical?
• Did you catch yourself acting irrational?
• Did you observe any phases in the game?
• Why do you think the game could be considered an analogy for war?

Auction 1: Results!